
Recall that in this study, 14 of the 16 ten-month-old infants chose the helper If these conditions aren’t met, you shouldn’t use the Wald method.
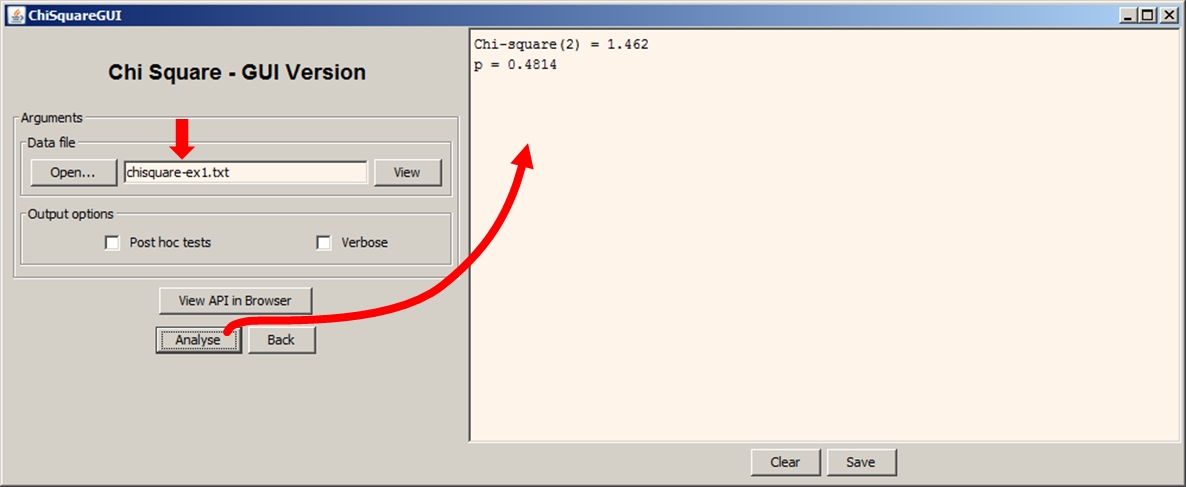
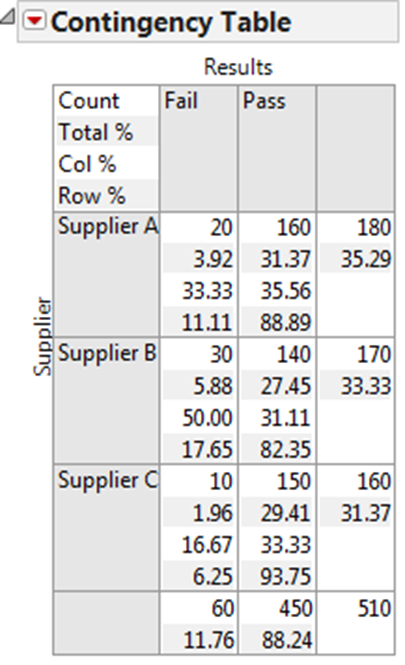
One rule of thumb is that as long as and, the Wald interval should work reasonably well. Other alternatives (such as adjusted Wald intervals, binomial exact intervals, or score intervals) will be more appropriate in these case. If our point estimate had been and the sample size had been n = 20, then the Wald method would not have provided us with a very reliable interval estimate of the true population proportion. For example, consider the binomial distribution with π =. This is because the normal curve does not approximate the binomial distribution very well in these situations. Note that this method does not typically perform well for very small sample sizes or when the point estimate is very close to either zero or one. We have considered a method known as the “Wald” interval. Several methods exist for constructing a confidence interval for a binomial proportion. Therefore, when available, a confidence interval should always accompany the hypothesis test. General Comments Concerning the Confidence Interval for a Single Proportion*:Ī confidence interval allows us to estimate the population parameter of interest (note that the hypothesis test does NOT allow us to do this). “middle” 95% of this distribution from the outer 5%. To get a 95% confidence interval for the parameter of interest, we findīoth the lower endpoint and the upper endpoint that separate the The distribution of sample proportions obtained by repeated sampling To change from one random sample to the next because of natural sampling Then, we can use Tinkerplots to get an idea of how much we expect this statistic To get this range of likely values, we’ll start with our pointĮstimate (i.e., the sample statistic, = 51%). Interest with a range of likely values (this range is called the confidence Point estimate, we’ll also use statistical methods to estimate the parameter of Polled, this point estimate would likely change. We know, however, that if a different sample of 800 Minnesotan adults had been Of all Minnesotans that feel medical marijuana should be legalized is What is the sample statistic of interest?īased on the results of this poll, our best guess for the proportion.Mind as you answer the following questions. The survey) that medical marijuana should be legalized. 001).Ultimately, the Star Tribune conducted this poll because they wanted toĮstimate the proportion of adults in Minnesota that felt (at the time of There was a significant association between class rank and living on campus ( Χ 2(1) = 138.9, p Since the p-value is less than our chosen significance level α = 0.05, we can reject the null hypothesis, and conclude that there is an association between class rank and whether or not students live on-campus.īased on the results, we can state the following: The corresponding p-value of the test statistic is so small that it is presented as p Because the crosstabulation is a 2x2 table, the degrees of freedom (df) for the test statistic is $$ df = (R - 1)*(C - 1) = (2 - 1)*(2 - 1) = 1 $$.The value of the test statistic is 138.926.We can confirm this computation with the results in the table labeled Statistics for Table of RankUpperUnder by LiveOnCampus: Computation of the expected cell counts and residuals (observed minus expected) for the crosstabulation of class rank by living on campus. With the Expected Count values shown, we can confirm that all cells have an expected value greater than 5. If you included the EXPECTED and DEVIATION options in your syntax, you should see the following: The first table in the output is the crosstabulation. TABLE RankUpperUnder*LiveOnCampus / CHISQ EXPECTED DEVIATION NOROW NOCOL NOPERCENT Suppose that we want to test the association between class rank and living on campus using a Chi-Square Test of Independence (using α = 0.05). The proportion of upperclassmen who live on campus is 5.6%, or 9/161.The proportion of upperclassmen who live off campus is 94.4%, or 152/161.The proportion of underclassmen who live on campus is 65.2%, or 148/227.The proportion of underclassmen who live off campus is 34.8%, or 79/227.Recall that the column percentages of the crosstab appeared to indicate that upperclassmen were less likely than underclassmen to live on campus: Let's continue the row and column percentage example from the Crosstabs tutorial, which described the relationship between the variables RankUpperUnder (upperclassman/underclassman) and LivesOnCampus (lives on campus/lives off-campus).


 0 kommentar(er)
0 kommentar(er)
